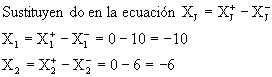VARIANTES EN LAS APLICACIONES SIMPLEX.
Existen casos especiales que se encuentran a menudo en las aplicaciones del método simplex, los más importantes son:
1. Degeneración.
2. Soluciones óptimas múltiples.
3. Soluciones óptimas no acotadas.
4. Soluciones factibles no existentes.
5. Variables no restringidas en signo.
1. DEGENERACION.
Un empate al elegir la variable que sale se rompe arbitrariamente. El problema ocurre en la siguiente iteración donde los valores de una o más variables básicas llegan a ser cero, en cuyo caso se dice que la solución es degenerada. En este punto no existe la seguridad de que el valor de la función objetivo mejorará, ya que la nueva solución óptima puede permanecer degenerada de ser así, es posible que las iteraciones del simplex entren en un circuito que repetirá las misma(as) sucesión de iteraciones sin alcanzar nunca la óptima.
El problema se conoce como ciclaje y afortunadamente raras veces se presenta en la práctica. En una situación de degeneración es esencial llevar las iteraciones del método simplex hasta que se satisfaga completamente la condición de optimidad.
EJEMPLO:
Maximizar ![]()
Sujeto a:
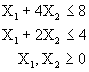
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-3 |
-9 |
0 |
0 |
0 |
|
S1 |
0 |
1 |
4 |
1 |
0 |
8 |
|
S2 |
0 |
1 |
2 |
0 |
1 |
4 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-3/4 |
0 |
9/4 |
0 |
18 |
|
X2 |
0 |
1/4 |
1 |
1/4 |
0 |
2 |
|
S2 |
0 |
1/2 |
0 |
-1/2 |
1 |
0 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
3/2 |
3/2 |
18 |
|
X2 |
0 |
0 |
1 |
1/2 |
-1/2 |
2 |
|
S2 |
0 |
1 |
0 |
-1 |
2 |
0 |
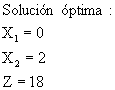
|
X1 |
X2 |
S1 |
S2 |
Z |
|
|
Tabla 1 |
0 |
0 |
8 |
4 |
0 |
|
Tabla 2 |
0 |
2 |
0 |
0 |
18 |
|
Tabla 3 |
0 |
2 |
0 |
0 |
18 |
EJEMPLO:
Maximizar ![]()
Sujeto a:
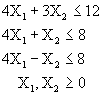
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
-2 |
-1 |
0 |
0 |
0 |
0 |
|
S1 |
0 |
4 |
3 |
1 |
0 |
0 |
12 |
|
S2 |
0 |
4 |
1 |
0 |
1 |
0 |
8 |
|
S3 |
0 |
4 |
-1 |
0 |
0 |
1 |
8 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
0 |
-1/2 |
0 |
1/2 |
0 |
4 |
|
S1 |
0 |
0 |
2 |
1 |
-1 |
0 |
4 |
|
X1 |
0 |
1 |
1/4 |
0 |
1/4 |
0 |
2 |
|
S3 |
0 |
0 |
-2 |
0 |
-1 |
1 |
0 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
0 |
0 |
1/4 |
1/4 |
0 |
5 |
|
S1 |
0 |
0 |
1 |
1/2 |
-1/2 |
0 |
2 |
|
S2 |
0 |
1 |
0 |
-1/8 |
3/8 |
0 |
3/2 |
|
S3 |
0 |
0 |
0 |
1 |
-2 |
1 |
4 |
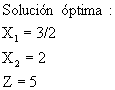
|
X1 |
X2 |
S1 |
S2 |
S3 |
Z |
|
|
Tabla 1 |
0 |
0 |
12 |
8 |
8 |
0 |
|
Tabla 2 |
2 |
0 |
4 |
0 |
0 |
4 |
|
Tabla 3 |
3/2 |
2 |
0 |
0 |
4 |
5 |
2. SOLUCIONES ÓPTIMAS MULTIPLES.
Existen problemas que tienen más de una solución óptima. En este caso se dice que se tienen soluciones óptimas múltiples debido a que la solución óptima se encuentra en un segmento de recta que es acotado por una de las restricciones.
Maximizar ![]()
Sujeto a:
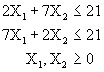
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-4 |
-14 |
0 |
0 |
0 |
|
S1 |
0 |
2 |
7 |
1 |
0 |
21 |
|
S2 |
0 |
7 |
2 |
0 |
1 |
21 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
2 |
0 |
42 |
|
X2 |
0 |
2/7 |
1 |
1/7 |
0 |
3 |
|
S2 |
0 |
4/7 |
0 |
-5/7 |
1 |
15 |
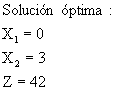
Nota: Si existe un cero en el primer renglón significa que hay soluciones óptimas múltiples.
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
2 |
0 |
42 |
|
X2 |
0 |
0 |
1 |
7/45 |
-2/45 |
7/3 |
|
X1 |
0 |
1 |
0 |
-2/45 |
7/45 |
7/3 |
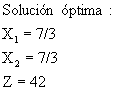
3. SOLUCIONES OPTIMAS NO ACOTADAS.
Existen problemas para los cuales una o más de las variables pueden aumentarse indefinidamente mejorando en forma indefinida la función objetivo. En esta situación, se dice que la solución óptima no está acotada, por lo que la solución óptima es infinita.
Maximizar ![]()
Sujeto a:
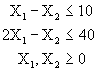
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-2 |
-1 |
0 |
0 |
0 |
|
S1 |
0 |
1 |
-1 |
1 |
0 |
10 |
|
S2 |
0 |
2 |
-1 |
0 |
1 |
40 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
-3 |
2 |
0 |
20 |
|
X1 |
0 |
1 |
-1 |
1 |
0 |
10 |
|
S2 |
0 |
0 |
1 |
-2 |
1 |
20 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
-4 |
3 |
80 |
|
X1 |
0 |
1 |
0 |
-1 |
1 |
30 |
|
S2 |
0 |
0 |
1 |
-2 |
1 |
20 |
No existe acotación para la variable. (Solución Optima no Acotada).
4. SOLUCIONES FACTIBLES NO EXISTENTES.
Existen problemas para los cuales no hay espacio de soluciones que cumplan con todas las restricciones. Este problema termina anotando que no existen soluciones factibles. Esta situación se identifica en la tabla del método simplex cuando se llega a la solución óptima y aún no desaparecen las variables artificiales.
Maximizar ![]()
Sujeto a:
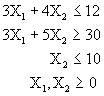
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
R1 |
Solución |
|
Z |
1 |
-4 |
-6 |
0 |
0 |
0 |
-M |
0 |
|
S1 |
0 |
3 |
4 |
1 |
0 |
0 |
0 |
12 |
|
R1 |
0 |
3 |
5 |
0 |
-1 |
0 |
1 |
30 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
R1 |
Solución |
|
Z |
1 |
-4+3M |
-6+5M |
0 |
-M |
0 |
0 |
30M |
|
S1 |
0 |
3 |
4 |
1 |
0 |
0 |
0 |
12 |
|
R1 |
0 |
3 |
5 |
0 |
-1 |
0 |
1 |
30 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
R1 |
Solución |
|
Z |
1 |
1/ 2-3/4M |
0 |
3/2-5/4M |
-M |
0 |
0 |
18+15m |
|
S1 |
0 |
3/ 4 |
1 |
1/ 4 |
0 |
0 |
0 |
3 |
|
R1 |
0 |
-3/4 |
0 |
-5/4 |
-1 |
0 |
1 |
15 |
|
S3 |
0 |
-3/4 |
0 |
-1/4 |
0 |
1 |
0 |
7 |
No existen soluciones factibles del problema.
No existe ninguna combinación de valores de X1 y X2 que satisfagan todas las restricciones.
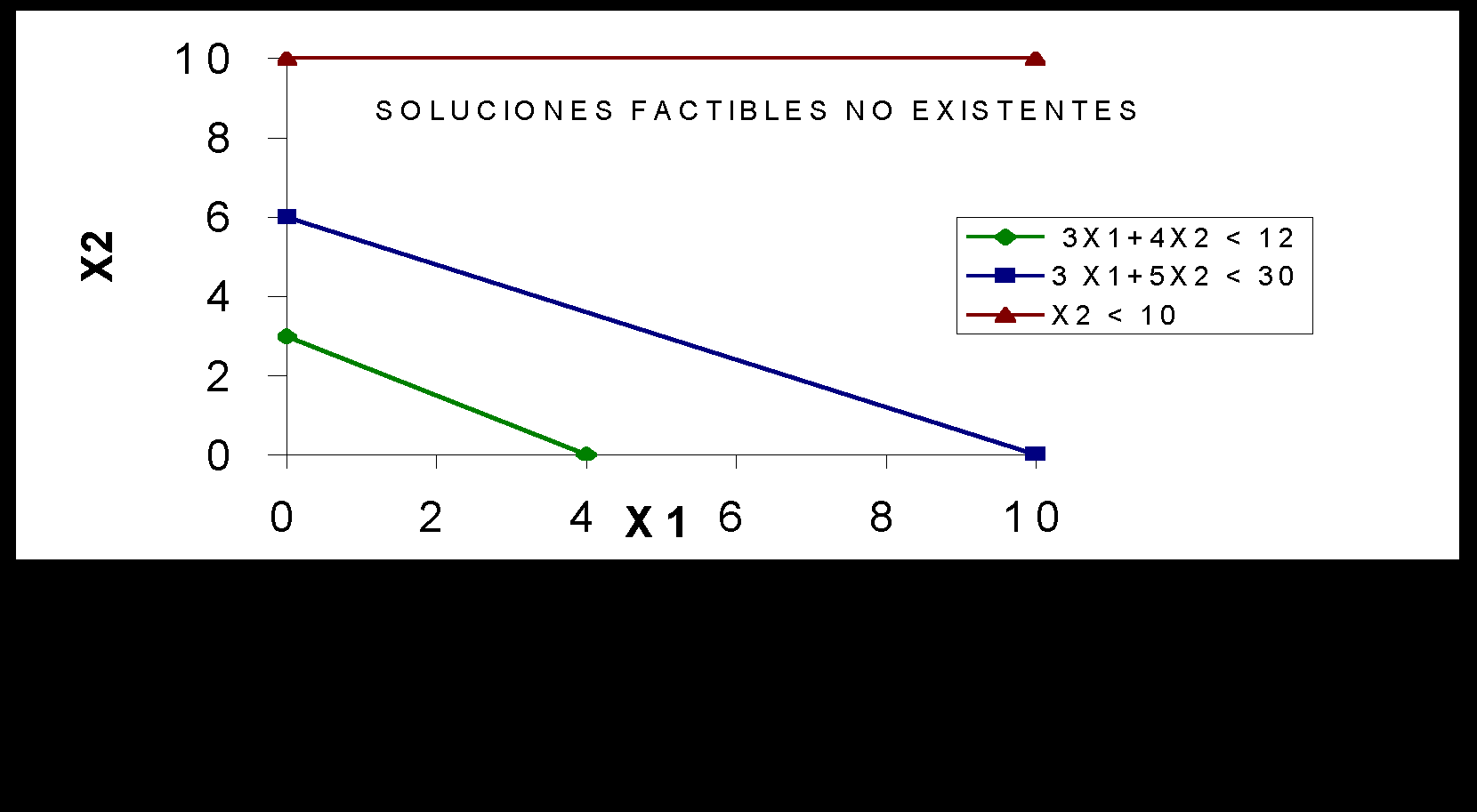
5. VARIABLES NO RESTRINGIDAS EN SIGNO
La programación lineal exige que las variables sean no negativas, pero existen algunas variables reales que pueden incluir valores negativos. Esta dificultad puede resolverse transformando cada variable no restringida en signo por dos nuevas variables no negativas mediante la siguiente expresión:
![]()
Se resuelve el problema empleando los métodos ya conocidos. La solución del problema original se determina a partir de la solución del problema modificado empleando la misma relación.
EJEMPLO:
Encuentre la solución óptima del siguiente modelo con variables irrestrictas en signo.
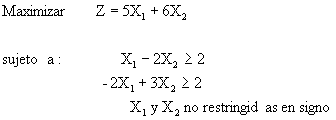
FASE 1.
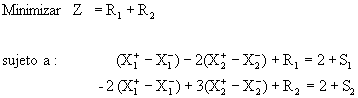

|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
|
R1 |
0 |
1 |
-1 |
-2 |
2 |
-1 |
0 |
1 |
0 |
2 |
|
R2 |
0 |
-2 |
2 |
3 |
-3 |
0 |
-1 |
0 |
1 |
2 |
|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
-1 |
1 |
1 |
-1 |
-1 |
-1 |
0 |
0 |
4 |
|
R1 |
0 |
1 |
-1 |
-2 |
2 |
-1 |
0 |
1 |
0 |
2 |
|
R2 |
0 |
-2 |
2 |
3 |
-3 |
0 |
-1 |
0 |
1 |
2 |
|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
-1/2 |
+1/2 |
-1 |
-1/2 |
0 |
-1/2 |
3 |
|
R1 |
0 |
0 |
0 |
-1/2 |
+1/2 |
-1 |
-1/2 |
1 |
+1/2 |
3 |
|
X1- |
0 |
-1 |
1 |
3/2 |
-3/2 |
0 |
-1/2 |
0 |
+1/2 |
1 |
|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
|
X2- |
0 |
0 |
0 |
-1 |
1 |
-2 |
-1 |
2 |
1 |
6 |
|
X1- |
0 |
-1 |
1 |
0 |
0 |
-3 |
-2 |
3 |
2 |
10 |
FASE 2.
![]()
![]()
|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
Solución |
|
Z |
1 |
-5 |
5 |
-6 |
6 |
0 |
0 |
0 |
|
X2- |
0 |
0 |
0 |
-1 |
1 |
-2 |
-1 |
6 |
|
X1- |
0 |
-1 |
1 |
0 |
0 |
-3 |
-2 |
10 |
|
V. básica |
Z |
X1+ |
X1- |
X2+ |
X2- |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
27 |
16 |
-86 |
|
X2- |
0 |
0 |
0 |
-1 |
1 |
-2 |
-1 |
6 |
|
X1- |
0 |
-1 |
1 |
0 |
0 |
-3 |
-2 |
10 |
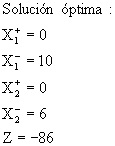
![]()