PROCEDIMIENTO.
1. El método requiere que las restricciones sean ecuaciones (relaciones de igualdad). Cualquier inecuación puede ser convertida en una ecuación agregando una cantidad negativa en el lado de menor valor de la inecuación.
Esta variable se llama variable de holgura y también se introduce en la función objetivo con coeficiente cero ya que no influye en el valor de la función objetivo.
2. Encontrar una solución básica factible inicial para el sistema de ecuaciones.
En muchos casos, las variables de holgura representan una solución obvia de inicio porque sus coeficientes forman una matriz identidad, donde los elementos diagonales son unos y los elementos restantes son ceros. Además, los valores del lado derecho de las ecuaciones siempre son negativos.
Una forma conveniente de registrar la información sobre la solución de inicio es utilizar una tabla.
En esta tabla la función objetivo se expresa como una ecuación igualada a cero. En esta tabla existe la columna variable básica que contiene la identificación de cuales son las variables básicas de la solución actual. Las variables no básicas actuales no aparecen en esta columna y sus valores son cero.
3. Encontrar una solución básica factible mejor.
Esta es una fase iterativa donde se busca una solución mejor que la actual. En este paso se busca identificar una variable básica que mejore la función objetivo. Esta variable se llama "variable básica entrante" y reemplazarla por otra variable básica llamada "variable básica saliente".
La condición de optimidad estipula que la variable que entra será elegida como la variable no básica que tenga un coeficiente negativo más grande en la ecuación de la función objetivo (Z) de la tabla para problemas de maximización y el coeficiente positivo más grande para minimización.
La variable básica que sale es la que representa la relación mínima positiva de cocientes entre la columna solución y la columna variable básica entrante.
4. Formar una nueva tabla con la solución mejorada para crear la nueva tabla de soluciones se identifica la columna pivote que está señalada por la variable básica que entra. También se identifica el renglón pivote que está indicado por la variable básica que sale. El valor que forma el cruce de la columna pivote y el renglón pivote se llama elemento pivote. Se obtiene el nuevo renglón pivote dividiendo el renglón anterior por el coeficiente del elemento pivote. Se generan ceros en todos los valores de la nueva columna pivote realizando operaciones entre los renglones anteriores y el renglón pivote nuevo.
5.Buscar una solución básica factible mejor.
Si existe una solución básica factible mejor, se vuelve a formar una nueva tabla de soluciones. Si no se puede encontrar una solución, la solución obtenida es óptima. El criterio de búsqueda de mejores soluciones ya se señaló en el paso 3.
EJERCICIO.
Resuelva el problema de la familia de contadores utilizando el método simplex.
Maximizar ![]()
Sujeto a:
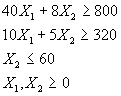
El modelo se transforma de un sistema de inecuaciones a uno de ecuaciones agregando variables de holgura al lado de menor valor de las inecuaciones. Estas variables tendrán una aportación de cero en la función objetivo.
Maximizar ![]()
Sujeto a:
![]()
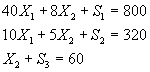
La función objetivo se iguala a cero para formar la tabla.
Maximizar ![]()
Sujeto a:
![]()
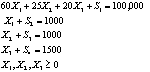
Se genera una tabla inicial creando una columna para cada variable del modelo. Además, se agrega la columna variable básica donde se mencionan las variables que forman parte de la solución actual. La columna solución se obtiene de los términos independientes del modelo y representa el valor de las variables básicas.
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
-300 |
-100 |
0 |
0 |
0 |
0 |
|
S1 |
0 |
40 |
8 |
1 |
0 |
0 |
800 |
|
S2 |
0 |
10 |
5 |
0 |
1 |
0 |
320 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
1 |
60 |
REQUISITOS PARA IDENTIFICAR LA SOLUCION BASICA FACTIBLE DE INICIO:
1. Existe la matriz identidad.
2. Valores de la columna solución son no negativos.
3. Cumple con las restricciones.
4. Es un vértice del área de soluciones factibles.
La solución inicial está dada por los siguientes valores:
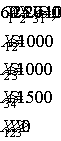
El valor mayor negativo (Z) es de la variable entrante. El cruce entre el renglón y la columna pivote se llama elemento pivote.
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
0 |
-40 |
15/2 |
0 |
0 |
6000 |
|
X1 |
0 |
1 |
1/5 |
1/40 |
0 |
0 |
20 |
|
S2 |
0 |
0 |
3 |
-1/4 |
1 |
0 |
120 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
1 |
60 |
El procedimiento es iterativo hasta que no existan variables entrantes (para un problema de maximización la mayor negativa en el renglón Z).
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
0 |
-40 |
15/2 |
0 |
0 |
6000 |
|
X1 |
0 |
1 |
1/5 |
1/40 |
0 |
0 |
20 |
|
S2 |
0 |
0 |
3 |
-1/4 |
1 |
0 |
120 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
1 |
60 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
S3 |
Solución |
|
Z |
1 |
0 |
0 |
25/6 |
40/3 |
0 |
7600 |
|
X1 |
0 |
1 |
0 |
1/24 |
-1/15 |
0 |
12 |
|
X2 |
0 |
0 |
1 |
-1/12 |
1/3 |
0 |
40 |
|
S3 |
0 |
0 |
0 |
1/12 |
-1/3 |
1 |
20 |
Aquí ya no aparecen coeficientes negativos en el renglón Z, por lo tanto la solución actual será óptima.

![]()
PROBLEMA 2.
Suponga que usted es el presidente de una firma de inversiones personales y que maneja cierta cartera de valores de cierto número de clientes. Un cliente nuevo ha solicitado recientemente que la firma le maneje una cartera de $100,000. Al cliente le gustaría limitar su cartera a una combinación de las 3 acciones que se muestran en al figura. Determinar cuantas acciones de cada tipo debería comprar para maximizar el beneficio total anual estimado.
|
Acción |
Precio por Acción |
Beneficio anual estimado |
Máxima inversión posible |
|
A |
$60 |
$7 |
60,000 |
|
B |
$25 |
$3 |
25,000 |
|
C |
$20 |
$3 |
30,000 |
OBJETIVO : Maximizar el beneficio total anual estimado
RESTRICCIONES : Dinero disponible.
Máxima inversión posible
VARIABLE DE DECISION: Cantidad de acciones a comprar tipo A. (X1).
Cantidad de acciones a comprar tipo B. (X2).
Cantidad de acciones a comprar tipo C. (X3).
Maximizar ![]()
Sujeto a:
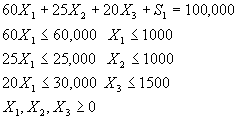
Maximizar ![]()
Sujeto a:
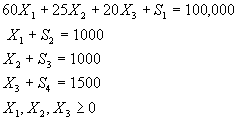
Maximizar ![]()
Sujeto a:
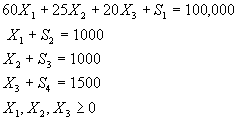
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
Solución |
|
Z |
1 |
-7 |
-3 |
-3 |
0 |
0 |
0 |
0 |
0 |
|
S1 |
0 |
60 |
25 |
20 |
1 |
0 |
0 |
0 |
100,000 |
|
S2 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1000 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
|
S4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1500 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
Solución |
|
Z |
1 |
0 |
-3 |
-3 |
0 |
7 |
0 |
0 |
7000 |
|
S1 |
0 |
0 |
25 |
20 |
1 |
-60 |
0 |
0 |
40,000 |
|
X1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1000 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
|
S4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1500 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
Solución |
|
Z |
1 |
0 |
-3 |
0 |
0 |
7 |
0 |
3 |
11,500 |
|
S1 |
0 |
0 |
25 |
0 |
1 |
-60 |
0 |
-20 |
10,000 |
|
X1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1000 |
|
S3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
|
X3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1500 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
3/25 |
-1/5 |
0 |
3/5 |
12,700 |
|
X2 |
0 |
0 |
1 |
0 |
1/25 |
-12/5 |
0 |
-4/5 |
400 |
|
X1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1000 |
|
S3 |
0 |
0 |
0 |
0 |
-1/25 |
12/5 |
1 |
4/5 |
6000 |
|
X3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1500 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
7/60 |
0 |
1/12 |
2/3 |
12,750 |
|
X2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1000 |
|
X1 |
0 |
1 |
0 |
0 |
1/60 |
0 |
-5/12 |
-1/3 |
750 |
|
S3 |
0 |
0 |
0 |
0 |
-1/60 |
1 |
5/12 |
1/3 |
250 |
|
X3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1500 |
