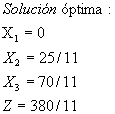METODO DE LAS DOS FASES.
La desventaja de la técnica M es el posible error de cómputo que podría resultar de asignar un valor muy grande a la constante M. Esta situación podría presentar errores de redondeo en las operaciones de la computadora digital. Para evitar esta dificultad el problema se puede resolver en 2 fases.
FASE 1. Formule un nuevo problema reemplazando la función objetivo por la suma de las variables artificiales.
La nueva función objetivo se minimiza sujeta a las restricciones del problema original. Si el problema tiene un espacio factible el valor mínimo de la función objetivo óptima será cero, lo cual indica que todas las variables artificiales son cero. En este momento pasamos a la fase 2.
* Si el valor mínimo de la función objetivo óptima es mayor que cero, el problema no tiene solución y termina anotándose que no existen soluciones factibles
FASE 2. Utilice la solución óptima de la fase 1 como solución de inicio para el problema original. En este caso, la función objetivo original se expresa en términos de las variables no básicas utilizando las eliminaciones usuales Gauss-Jordan.
PROBLEMA # 1
Minimizar ![]()
Sujeto a:
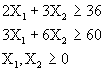
Minimizar ![]()
Sujeto a:
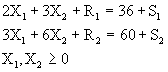
FASE I
Minimizar ![]()
Sujeto a:
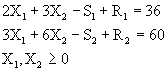
Minimizar ![]()
Sujeto a:
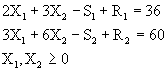
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
|
R1 |
0 |
2 |
3 |
-1 |
0 |
1 |
0 |
36 |
|
R2 |
0 |
3 |
6 |
0 |
-1 |
0 |
1 |
60 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
5 |
9 |
-1 |
-1 |
0 |
0 |
96 |
|
R1 |
0 |
2 |
3 |
-1 |
0 |
1 |
0 |
36 |
|
R2 |
0 |
3 |
6 |
0 |
-1 |
0 |
1 |
60 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
1/2 |
0 |
-1 |
1 /2 |
0 |
3/2 |
6 |
|
R1 |
0 |
1/2 |
0 |
-1 |
1 /2 |
1 |
-1/2 |
6 |
|
X2 |
0 |
1/2 |
1 |
0 |
-1/6 |
0 |
1/6 |
10 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
|
X1 |
0 |
1 |
0 |
-2 |
1 |
2 |
-1 |
12 |
|
X2 |
0 |
0 |
1 |
1 |
-2/3 |
-1 |
2/3 |
4 |
FASE II.
Minimizar ![]()
![]()
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-2000 |
-500 |
0 |
0 |
0 |
|
X1 |
0 |
1 |
0 |
-2 |
1 |
12 |
|
X2 |
0 |
0 |
1 |
1 |
-2/3 |
4 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
0 |
0 |
-3500 |
5000/3 |
26000 |
|
X1 |
0 |
1 |
0 |
-2 |
1 |
12 |
|
X2 |
0 |
0 |
1 |
1 |
-2/3 |
4 |
|
V. Básica |
Z |
X1 |
X2 |
S1 |
S2 |
Solución |
|
Z |
1 |
-5000/3 |
0 |
-500/3 |
0 |
6000 |
|
S2 |
0 |
1 |
0 |
-2 |
1 |
12 |
|
X2 |
0 |
2/3 |
1 |
-1/3 |
0 |
12 |
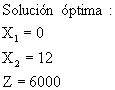
PROBLEMA 2.
Maximizar ![]()
Sujeto a:
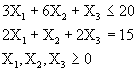
FASE I.
En la FASE I siempre es un problema de minimización.
Minimizar ![]()
Sujeto a:
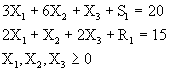
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
R1 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
S1 |
0 |
3 |
6 |
1 |
1 |
0 |
20 |
|
R1 |
0 |
3 |
1 |
2 |
0 |
1 |
15 |
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
R1 |
Solución |
|
Z |
1 |
3 |
1 |
2 |
0 |
-1 |
15 |
|
S1 |
0 |
3 |
6 |
1 |
1 |
0 |
20 |
|
R1 |
0 |
3 |
1 |
2 |
0 |
1 |
15 |
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
R1 |
Solución |
|
Z |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
S1 |
0 |
0 |
5 |
-1 |
1 |
-1 |
5 |
|
X1 |
0 |
1 |
1/3 |
2/3 |
0 |
1/3 |
5 |
Aquí termina la fase I.
FASE II.
Maximizar ![]()
![]()
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
Solución |
|
Z |
1 |
-6 |
-4 |
-4 |
0 |
0 |
|
S1 |
0 |
0 |
5 |
-1 |
1 |
5 |
|
X1 |
0 |
1 |
1/3 |
2/3 |
0 |
5 |
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
Solución |
|
Z |
1 |
0 |
-2 |
0 |
0 |
30 |
|
S1 |
0 |
0 |
5 |
-1 |
1 |
5 |
|
X1 |
0 |
1 |
1/3 |
2/3 |
0 |
5 |
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
Solución |
|
Z |
1 |
0 |
0 |
-2/5 |
2/5 |
32 |
|
X2 |
0 |
0 |
1 |
-1/5 |
1/5 |
1 |
|
X1 |
0 |
1 |
0 |
11/15 |
-1/15 |
14/3 |
|
V. Básica |
Z |
X1 |
X2 |
X3 |
S1 |
Solución |
|
Z |
1 |
6/11 |
0 |
0 |
4/11 |
380/11 |
|
X2 |
0 |
3/11 |
1 |
0 |
2/11 |
25/11 |
|
X1 |
0 |
15/11 |
0 |
1 |
-5/11 |
70/11 |