UNIDAD V.

MODELO DE TRANSPORTE.

Un problema de transporte incluye m fuentes, a cada una de las cuales corresponde una disponibilidad de a (i=1,2,3,...,m) unidades de un producto y n destinos, cada uno de los cuales requiere b (j=1,2,3,...,n) unidades de este producto.

Los números de ay bson enteros positivos. El costo Cde transportar una unidad de producto de la fuente al destino, se da para cada valor de y para cada valor de . El objetivo es desarrollar un programa de transporte que cumpla todas las demandas con un costo de embarque mínimo se considera que el suministro total y la demanda total son iguales esto es:

Se garantiza que la ecuación anterior se cumpla creando destinos ficticios con una demanda igual al excedente, si la demanda total es menor que el suministro total, a un origen ficticio con un suministro igual al faltante, si la demanda total excede al suministro total.

El modelo matemático del problema es un modelo de programación lineal dado por:

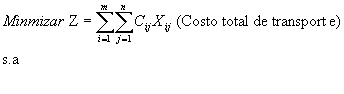
= Costo de transporte de enviar un artículo desde el origen i al destino j

= Cantidad de artículos enviados desde el origen i al destino j

= Cantidad de artículos disponibles en el origen i

= Cantidad de artículos requeridos por el destino j

m = Número de fuentes

n= Número de destinos

Por medio de la aplicación directa del método simplex siempre se obtiene la solución óptima, pero a veces resulta más eficiente trabajar con modelos especiales de transporte.

A fin de apreciar la estructura del modelo de transporte se considera un ejemplo con 2 orígenes (m=2) y 3 destinos (n=3).

s.a.

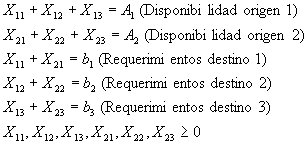
BALANCEO DEL MODELO DE TRANSPORTE.

La definición del general modelo de transporte implica que:

Esto significa que la oferta de todos los orígenes debe igualar a la demanda de todos los destinos. En problemas reales esta restricción no necesita satisfacerse siempre. La oferta disponible puede ser menor que la demanda o puede excederla. En este caso se dice que el problema no está balanceado. El balance de un problema de transporte es fundamental para desarrollar la técnica. Sin embargo, cualquier problema real puede balancearse artificialmente convirtiendolo en un problema con igual oferta y demanda.

Si la demanda excede a la oferta, se aumenta un origen ficticio que suministrará

Si existe exceso de oferta, se utiliza un destino ficticio para absorber la cantidad excedente

Los costos de transporte por unidad desde el origen ficticio a los destinos son cero, ya que esto equivale a no transportar desde el origen. En forma semejante se trabaja para los destinos ficticios.

TECNICAS DE TRANSPORTE.

Los pasos básicos de un modelo de transporte son:

1. Encontrar una solución básica inicial.

2. Mejorar esa solución inicial hasta encontrar la solución óptima.