UNIDAD V.
MODELO DE TRANSPORTE.
Un problema de transporte incluye m fuentes, a cada una de las cuales corresponde una disponibilidad de a![]() (i=1,2,3,...,m) unidades de un producto y n destinos, cada uno de los cuales requiere b
(i=1,2,3,...,m) unidades de un producto y n destinos, cada uno de los cuales requiere b![]() (j=1,2,3,...,n) unidades de este producto.
(j=1,2,3,...,n) unidades de este producto.
Los números de a![]() y b
y b![]() son enteros positivos. El costo C
son enteros positivos. El costo C![]() de transportar una unidad de producto de la fuente
de transportar una unidad de producto de la fuente ![]() al destino
al destino![]() , se da para cada valor de
, se da para cada valor de ![]() y para cada valor de
y para cada valor de![]() . El objetivo es desarrollar un programa de transporte que cumpla todas las demandas con un costo de embarque mínimo se considera que el suministro total y la demanda total son iguales esto es:
. El objetivo es desarrollar un programa de transporte que cumpla todas las demandas con un costo de embarque mínimo se considera que el suministro total y la demanda total son iguales esto es:
![]()
Se garantiza que la ecuación anterior se cumpla creando destinos ficticios con una demanda igual al excedente, si la demanda total es menor que el suministro total, a un origen ficticio con un suministro igual al faltante, si la demanda total excede al suministro total.
El modelo matemático del problema es un modelo de programación lineal dado por:
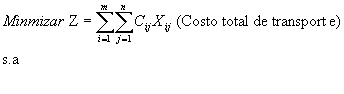

![]() = Costo de transporte de enviar un artículo desde el origen i al destino j
= Costo de transporte de enviar un artículo desde el origen i al destino j
![]() = Cantidad de artículos enviados desde el origen i al destino j
= Cantidad de artículos enviados desde el origen i al destino j
![]() = Cantidad de artículos disponibles en el origen i
= Cantidad de artículos disponibles en el origen i
![]() = Cantidad de artículos requeridos por el destino j
= Cantidad de artículos requeridos por el destino j
m = Número de fuentes
n= Número de destinos
Por medio de la aplicación directa del método simplex siempre se obtiene la solución óptima, pero a veces resulta más eficiente trabajar con modelos especiales de transporte.
A fin de apreciar la estructura del modelo de transporte se considera un ejemplo con 2 orígenes (m=2) y 3 destinos (n=3).
|
C 11 |
C 12 |
C 13 |
|||||||
|
X 11 |
X 12 |
X 13 |
A1 |
||||||
|
C 21 |
C 22 |
C 23 |
|||||||
|
X 21 |
X 22 |
X 23 |
A2 |
||||||
|
b1 |
b2 |
b3 |
![]()
s.a.
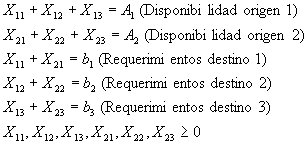
BALANCEO DEL MODELO DE TRANSPORTE.
La definición del general modelo de transporte implica que:
Esto significa que la oferta de todos los orígenes debe igualar a la demanda de todos los destinos. En problemas reales esta restricción no necesita satisfacerse siempre. La oferta disponible puede ser menor que la demanda o puede excederla. En este caso se dice que el problema no está balanceado. El balance de un problema de transporte es fundamental para desarrollar la técnica. Sin embargo, cualquier problema real puede balancearse artificialmente convirtiendolo en un problema con igual oferta y demanda.
Si la demanda excede a la oferta, se aumenta un origen ficticio que suministrará
![]()
Si existe exceso de oferta, se utiliza un destino ficticio para absorber la cantidad excedente
![]()
![]()
Los costos de transporte por unidad desde el origen ficticio a los destinos son cero, ya que esto equivale a no transportar desde el origen. En forma semejante se trabaja para los destinos ficticios.
TECNICAS DE TRANSPORTE.
Los pasos básicos de un modelo de transporte son:
1. Encontrar una solución básica inicial.
2. Mejorar esa solución inicial hasta encontrar la solución óptima.
METODOS PARA ENCONTAR UNA SOLUCION BASICA INICIAL.
En este capítulo analizaremos 3 procedimientos para encontrar una solución básica inicial a un problema de transporte. Los métodos son:
1. Método de la esquina del noroeste.
2. Método de costo mínimo.
3. Método de aproximación de vogel.
1. METODO DE LA ESQUINA NOROESTE.
Este método comienza asignando la cantidad máxima permisible para la oferta y la demanda a la variable X11 (la que está en la esquina noroeste de la tabla).
La columna o renglón satisfechos se tacha indicando que las variables restantes en la columna o renglón tachado son igual a cero. Si la columna y el renglón se satisfacen simultaneamente, únicamente uno (cualquiera de los dos) debe tacharse. Esta condición garantiza localizar las variables básicas cero si es que existen. Después de ajustar las cantidades de oferta y demanda para todos los renglones y columnas no tachados, la cantidad máxima factible se asigna al primer elemento no tachado en la nueva columna o renglón. El procedimiento termina cuando exactamente un renglón o una columna se dejan sin tachar.
Ejemplo:
Una compañía tiene 3 almacenes con 15, 25 y 5 artículos disponibles respectivamente. Con estos productos disponibles desea satisfacer la demanda de 4 clientes que requieren 5, 15, 15 y 10 unidades respectivamente. Los costos asociados con el envío de mercancía del almacén al cliente por unidad se dan en la siguiente tabla.
|
Clientes |
||||
|
Almacén |
1 |
2 |
3 |
4 |
|
1 |
10 |
0 |
20 |
11 |
|
2 |
12 |
7 |
9 |
20 |
|
3 |
0 |
14 |
16 |
18 |
Construya la solución básica inicial por el método de la esquina noroeste.

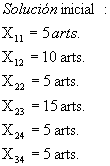
![]()
![]()
Ejemplo 2.
Una compañía de renta de autos tiene problemas de distribución debido a que los acuerdos de renta permiten que los autos se entreguen en lugares diferentes a aquellos en que originalmente fueron rentados. Por el momento, hay 2 lugares (fuentes) con 15 y 13 autos en exceso, respectivamente, y cuatro lugares (destinos) en los que se requieren 9, 6, 7, y 9 autos respectivamente. Los costos unitarios de transporte en dólares entre los lugares son los siguientes:
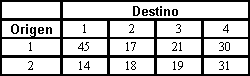
Elabore la tabla inicial de transporte por el método de la esquina noroeste.
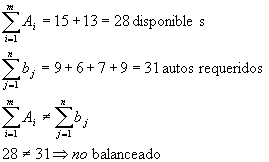
![]() Crear un origen ficticio con autos disponibles.
Crear un origen ficticio con autos disponibles.
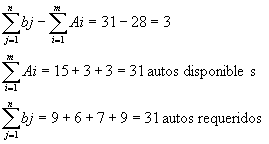
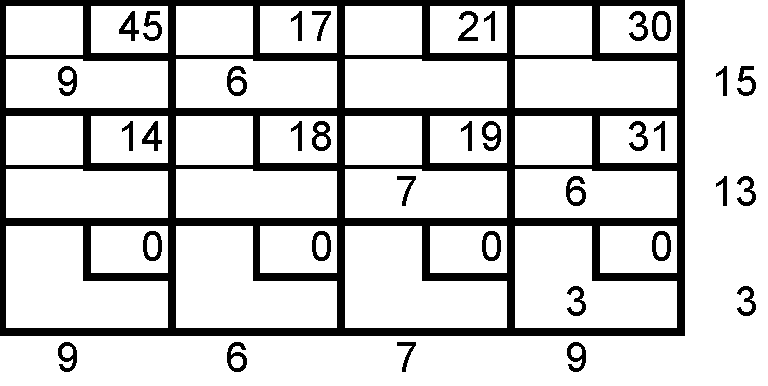
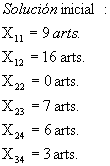
![]()
2. METODO DE COSTO MINIMO.
El método de costo mínimo trata de localizar una mejor solución inicial del modelo de transporte, utilizando las rutas baratas.
El procedimiento es como sigue: asigne tanto como sea posible a la variable con el costo unitario más pequeño en la tabla completa. Si la columna y el renglón se satisfacen simultáneamente únicamente uno puede ser tachado. Después ajuste la oferta y la demanda para todos los elementos no tachados, repita el proceso asignando tanto como sea posible a la variable no tachada con el costo unitario más pequeño. El procedimiento está completo cuando sólo un renglón o una columna están sin tachar.
Ejemplo:
Encuentre la solución básica inicial del ejemplo 1 utilizando el método del costo mínimo.
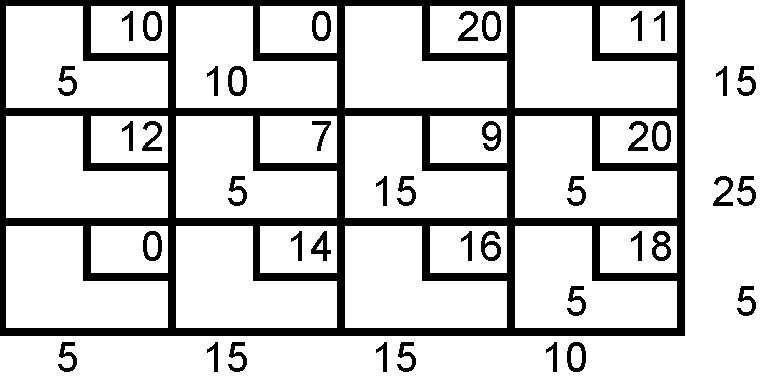
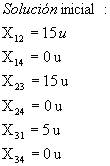
![]()
Ejemplo 2.
Una compañía de agua tiene 3 depósitos con una entrada diaria estimada de 15, 20 y 25 millones de litros de agua respectivamente. Diariamente tiene que abastecer 4 áreas A, B, C y D, las cuales tienen una demanda esperada de 8, 10, 12 y 15 millones de litros respectivamente. El costo de bombeo por millón de litros de agua es como sigue.
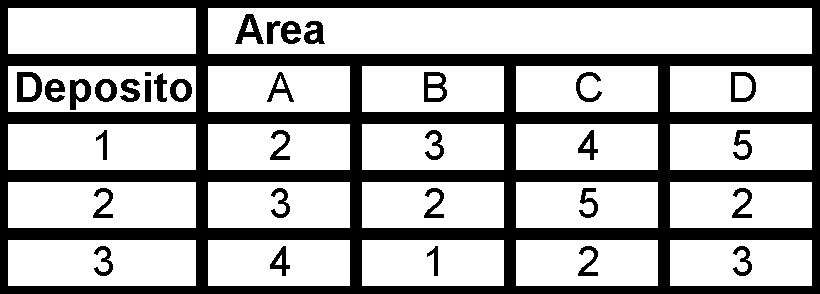
Encuentre la solución básica de inicio del modelo de transporte por el método de costo mínimo.
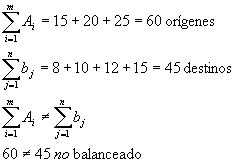
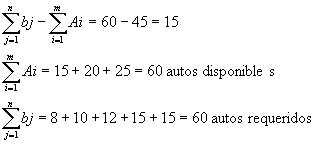
3. METODO DE APROXIMACION DE VOGEL.
Para cada renglón o columna en el que quede algún suministro o alguna demanda, calcúlese su diferencia, que es la diferencia no negativa entre los 2 más pequeños costos de embarque Cij asociadas con las variables no asignadas en ese renglón o en esa columna. Considérese el renglón o la columna para la mayor diferencia en caso de empate selecciónese uno arbitrariamente. En este renglón o columna localice la variable no asignada (celdilla) que tenga el costo unitario más pequeños de embarque y asígnele tantas unidades como sea posible sin ir en contra de las restricciones calcúlese las nuevas diferencias y repítase el procedimiento anterior hasta satisfacer todas las demandas.
Ejemplo:
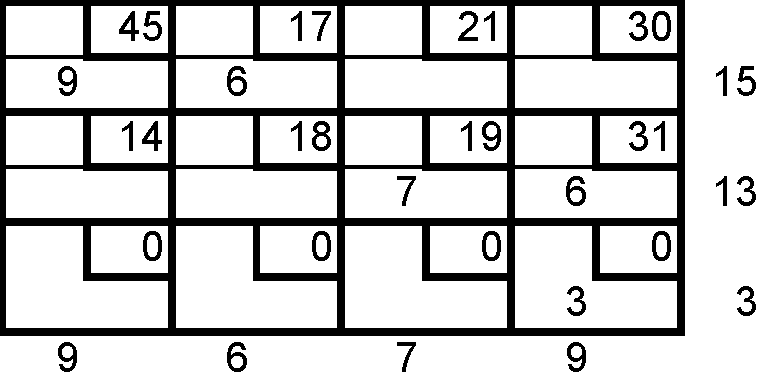
Encuentre la solución inicial del problema de la compañía de renta de autos por el método de aproximación de vogel.
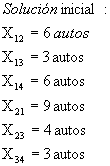
![]()
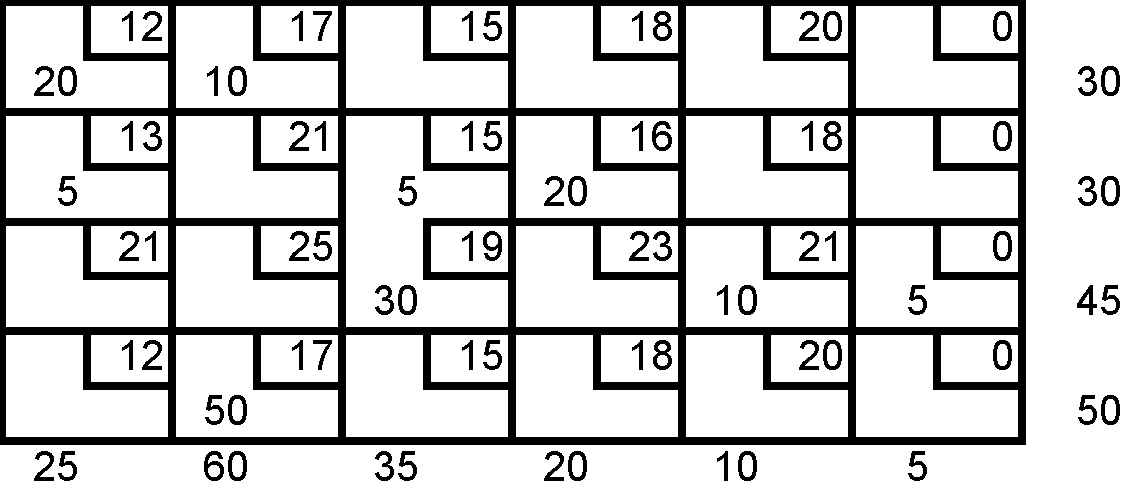
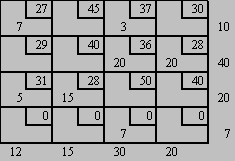
Una empresa está considerando satisfacer las necesidades de 4 clientes empleando los artículos que tiene disponibles en 3 almacenes. La cantidad de artículos que tiene en cada almacén son y es, 40 y 20 unidades respectivamente. Los clientes necesitan 12, 15, 30 y 20 unidades respectivamente. El costo unitario de embarque desde los almacenes hasta el cliente se encuentran en la siguiente tabla:

Encuentre la solución inicial del modelo de transporte utilizando el método de aproximación de vogel.
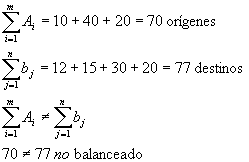
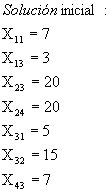
![]()
METODOS PARA ENCONTRAR LA SOLUCION OPTIMA DE UN MODELO DE TRANSPORTE.
1. METODO DE BANQUILLO.
La solución obtenida por los métodos anteriores es la solución inicial del método de banquillo. La forma de verificar si la solución actual puede mejorarse es examinar las variables no básicas actuales en busca de mejoras potenciales en el valor de la función objetivo. Si existe una de tales variables, será la variable que entra en cuyo caso una de las variables b{asicas actuales debe dejar la solución (como en el método simplex).
A fin de determinar la variable que entra y la que sale, se identifica un circuito cerrado para cada variable no básica. El circuito comienza y termina con la variable no básica designada. Un circuito consiste en segmentos horizontales y verticales sucesivos (conectados) cuyos puntos extremos deben ser variables básicas, excepto para los 2 segmentos de inicio y terminación en la variable no básica.
El circuito se utiliza para comprobar si el valor de la función objetivo puede mejorarse cuando la variable no básica se aumenta sobre su valor actual de cero.
El procedimiento consiste en encontrar el aumento o disminución en el costo de transporte como resultado de aumentar unidades en la variable no básica investigada.
Este valor se encuentra asignando signos positivos y negativos alternos en los costos asociados a las variables que forman el circuito, empezando con el costo de la variable no básica. La suma de los costos del circuito puede hacerse en el sentido de las manecillas del reloj o en sentido contrario.
El resultado obtenido en la suma de los costos del circuito puede ser positivo o negativo. Si es positivo indica que el asignar unidades a la variable que se está considerando aumenta el costo total de transporte. Pero si este valor es negativo, la solución puede mejorarse asignado a la variable no básica el valor más pequeño de las variables que deben reducir su valor en el circuito que se está considerando.
El procedimiento termina hasta que todas las variables no básicas tienen valor positivo en la suma de los costos del circuito.
Ejemplo:
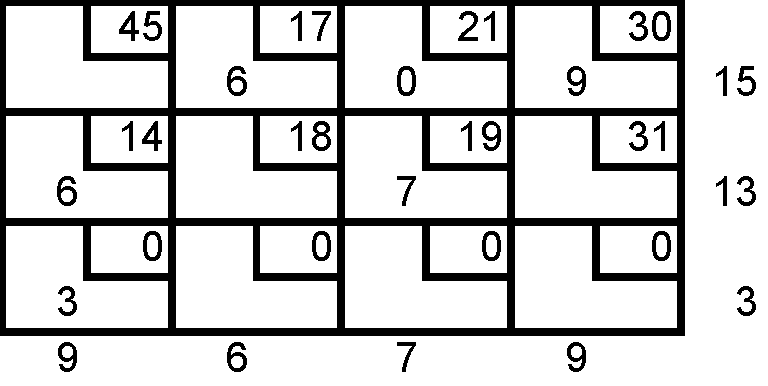
Encuentre la solución óptima del problema de la compañía de renta de autos utilizando una solución inicial por el método de costo mínimo y empleando el método de utilización de banquillo.
![]()
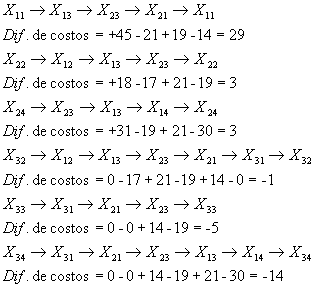
¿Cómo asignar?
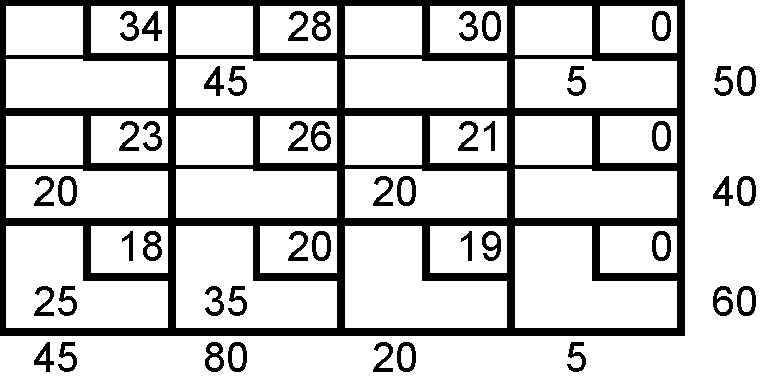
Restar 3 unidades a negativos y sumar 3 unidades a positivos.
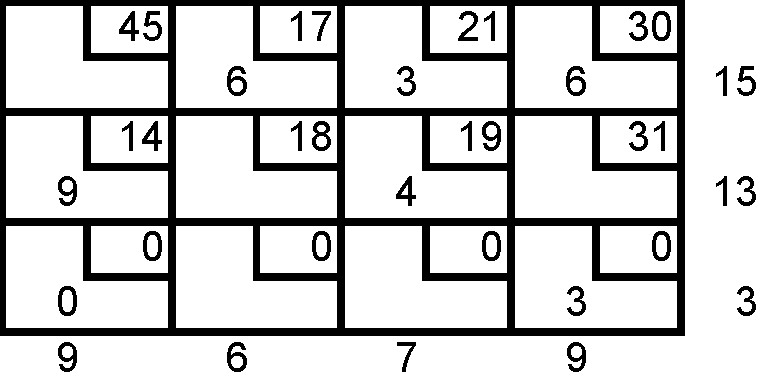
![]()
Se establecen nuevos criterios ó caminos
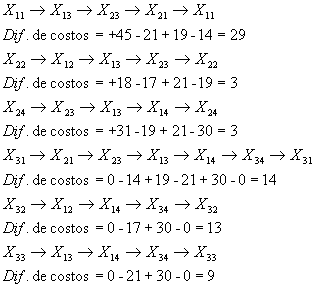
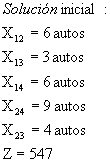
![]()
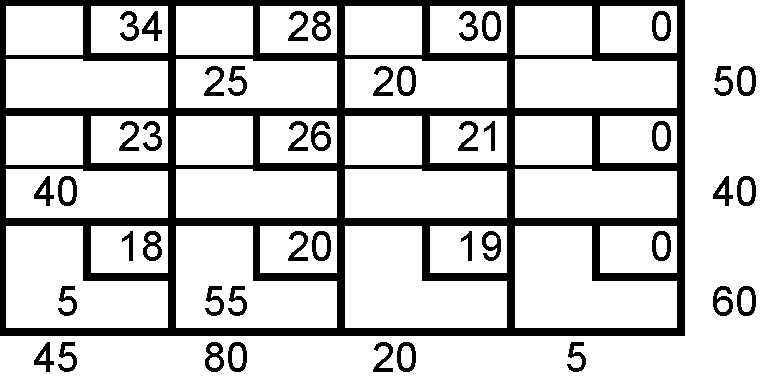
Dada la siguiente tabla inicial (método de aproximación de vogel) encuentre la solución óptima del modelo de transporte por el método de banquillo.

![]()

![]()

![]()
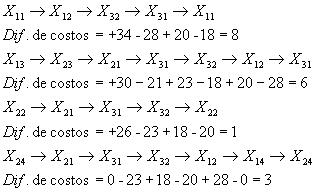
METODO DE MULTIPLICADORES (MODI).
Este método reproduce exactamente las mismas iteraciones del método de banquillo. La principal diferencia ocurre en la forma en que las variables no básicas se evalúan en cada iteración. Asociados a cada renglón i de la tabla existen multiplicadores Ui similarmente se asocia un multiplicador Vj a cada columna de la tabla j. Para cada variable básica Xij de la solución actual, se escribe la ecuación Ui +Vj = Cij. Esas ecuaciones proporcionan m+n-1 relaciones con m+n incógnitas.
Los valores de los multiplicadores pueden ser determinados a partir de las ecuaciones suponiendo un valor arbitrario para cualquiera de los multiplicadores (usualmente se establece U1=0) y resolviendo el sistema de ecuaciones para encontrar los multiplicadores desconocidos. Una vez que se hace esto, la evaluación de cada variable no básica X pq está dada como:
El criterio que se utiliza para seleccionar la variable que entra es el mismo que el método de banquillo (la mayor negativa).
Ejemplo:
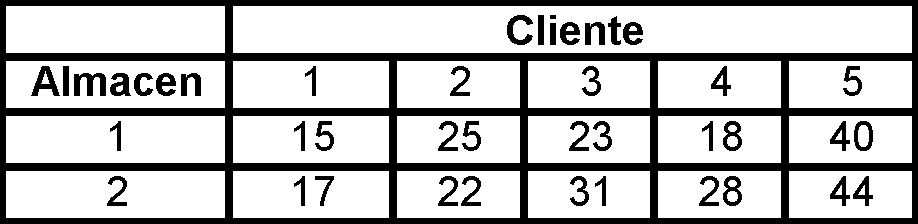
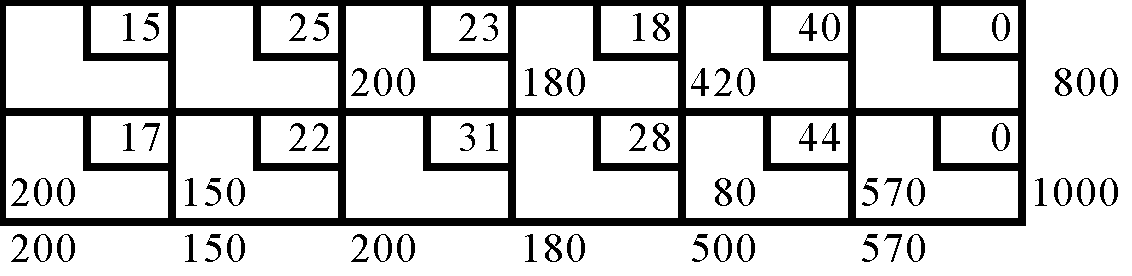
Una compañía está considerando una demanda de 5 clientes utilizando artículos que tienen disponibles en 2 almacenes. Los almacenes cuentan con 800 y 1000 unidades respectivamente. Los clientes necesitan 200, 150, 200, 180 y 500 unidades respectivamente. Los costos de embarque por artículo de los almacenes de los clientes son:
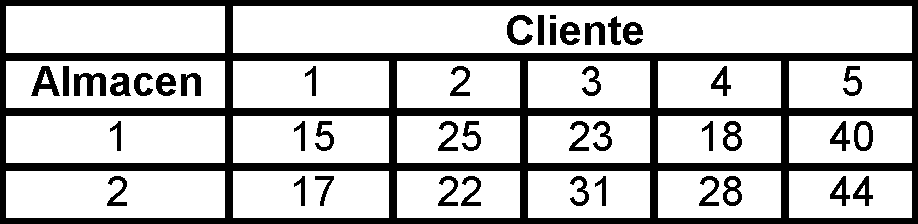
Resuelva el modelo de transporte empleando.
a) Una solución inicial por el método de aproximación de vogel.
b) La solución óptima por el método de multiplicadores.
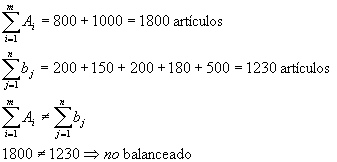
DESTINO FICTICIO = 570 ARTÍCULOS
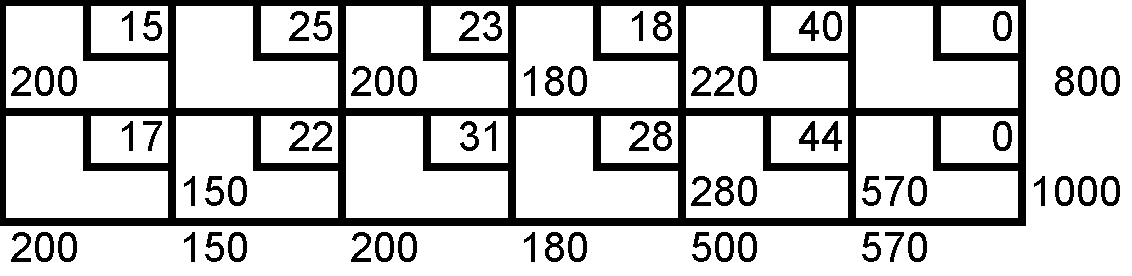
![]()
![]()
Para encontrar el valor de los multiplicadores
![]()
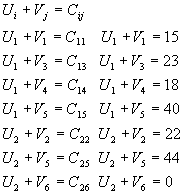
Se acostumbra:
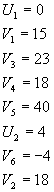
Para encontrar costos:
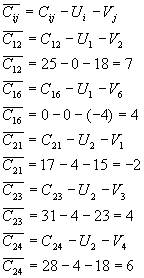
![]()
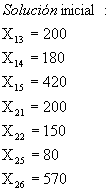
![]()
![]()
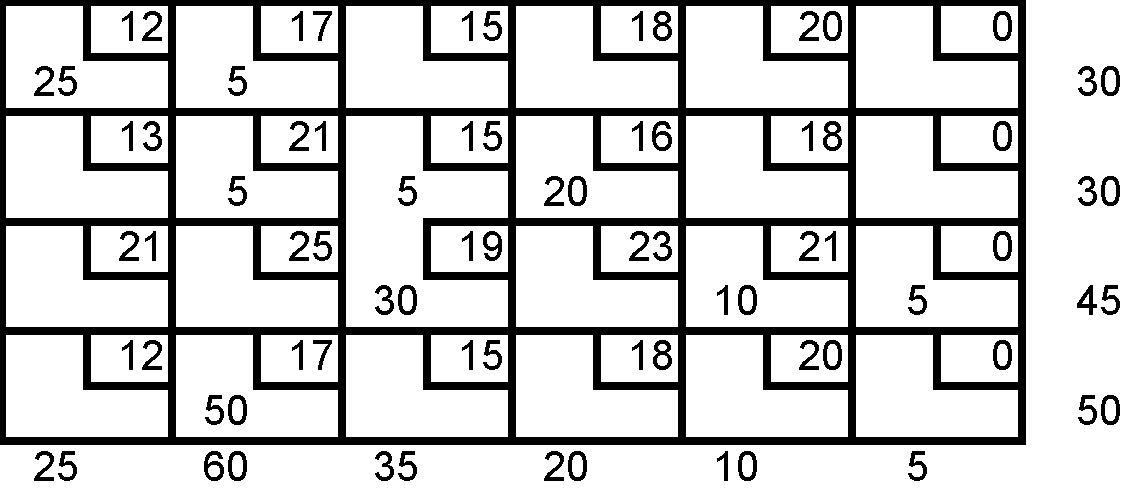
Encuentre la solución óptima por el método de multiplicadores a partir de la siguiente tabla inicial.
![]()
![]()