UNIDAD I
INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES
INVESTIGACIÓN DE OPERACIONES. Es un procedimiento científico que se encarga de analizar las actividades de un sistema de organización. El enfoque del estudio de Inv. De Operaciones está relacionado con la toma de decisiones para obtener el máximo aprovechamiento de recursos limitados.
MODELOS EN INVESTIGACIÓN DE OPERACIONES
MODELO. Es una representación de un sistema real. En Inv. de Operaciones se utilizan 3 tipos de modelos básicos para el estudio del problema.
1. Un modelo matemático o simbólico. Es el que se utiliza ecuaciones matemáticas para describir el comportamiento del sistema. Estas relaciones nos permiten conocer el comportamiento de las variables relevantes del sistema.
2. Modelos de Simulación. Es el que limita el comportamiento del sistema durante un período largo.
3. Modelos Heurísticos. Son aquellos que utilizan reglas empíricas para obtener una solución mejorada de un sistema real. (Por ejemplo: intervienen órdenes, máquinas, personas, no puede resolverse por medio de un modelo matemático).
FASES DE ESTUDIO DE INVESTIGACION DE OPERACIONES.
1. DEFINICION DEL PROBLEMA. Consiste en identificar la siguiente información:
a) Descripción de la meta u objetivo del estudio.
b) Identificación de las alternativas de decisión.
c) Reconocimiento de las limitaciones, restricciones y requisitos del sistema.
2. CONSTRUCCION DEL MODELO. Consiste en decidir cuál es el modelo más apropiado para representar el sistema.
3. SOLUCION DEL MODELO. Encontrar las variables que optimicen el sistema.
4. VALIDACION DEL MODELO. Consiste en comparar el funcionamiento del modelo con información que se tenga disponible del sistema real.
5. IMPLANTACION DE LOS RESULTADOS OBTENIDOS. Se trata de traducir las conclusiones del modelo en instrucciones detalladas para operar el nuevo sistema.
ESTRUCTURA DE LOS MODELOS MATEMATICOS.
Los modelos de programación lineal analizados en investigación de operaciones presentan la siguiente estructura.
1. FUNCION OBJETIVO.
Es la medida de la efectividad del sistema se expresa como una función matemática de las variables de decisión. La decisión óptima del modelo produce el mejor valor de la función objetivo.
2. RESTRICCIONES.
Son las limitaciones tecnológicas, económicas y otras del sistema que restringen las variables de decisión a un rango de valores factibles.
3. VARIABLES DE DECISION.
Son las incógnitas o las decisiones que deben tomarse resolviendo el modelo.
4. PARAMETROS DE DECISION.
Son valores conocidos que relacionan las variables con las restricciones o con la función objetivo.
Por ejemplo:
FORMULACION DE PROBLEMAS LINEALES.
La programación lineal son modelos destinados a la asignación eficiente de los recursos limitados en actividades conocidas con el objetivo de satisfacer las metas deseadas (maximizar beneficios o minimizar costos).
La característica distintiva de los modelos es que las funciones que representan el objetivo y las restricciones son lineales. (No se permite multiplicación de variables ni variables elevadas a potencias). Algunas de las siguientes restricciones no se pueden emplear en un modelo de programación lineal.
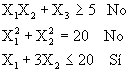
Un modelo de programación lineal se define usualmente como sigue:
Maximizar o minimizar ![]()
Sujeto a:
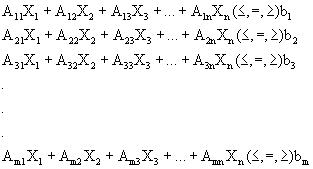
![]()

EJEMPLO 1.
Un fabricante de muebles tiene 6 unidades de maderas y 28 horas disponibles, durante las cuales fabricará biombos decorativos. Con anterioridad, se han vendido bien 2 modelos, de manera que se limitará a producir estos 2 tipos. Estima que el modelo uno requiere 2 unidades de madera y 7 horas de tiempo disponible, mientras que el modelo 2 requiere una unidad de madera y 8 horas. Los precios de los modelos son 120 dls. y 80 dls., respectivamente. ¿Cuántos biombos de cada modelo debe fabricar si desea maximizar su ingreso en la venta?
OBJETIVO : Maximizar el ingreso por ventas
RESTRICCIONES : Unidades de madera
Tiempo disponible
VARIABLE DE DECISION:
X1 = Cantidad de biombos tipo I a fabricar
X2 = Cantidad de biombos tipo II a fabricar
Maximizar ![]()
Sujeto a:
![]()
![]()
PROBLEMA 2.
Una firma de contadores públicos especializados en preparar liquidaciones y pago de impuestos y también auditorías en empresas pequeñas. El interés es saber cuantas auditorías y liquidaciones pueden realizar mensualmente, de tal manera que obtengan los máximos ingresos. Se dispone de 800 horas para trabajo directo y dirección y 320 horas para revisión. Una auditoría en promedio requiere de 40 horas de trabajo directo y dirección y 10 horas de revisión, además aporta un ingreso de 300 dls. Una liquidación de impuestos requiere de 8 horas de trabajo directo y dirección y 5 horas de revisión y produce un ingreso de 100 dls. Se pueden realizar tantas auditorías como se desee, pero el máximo de liquidaciones mensuales disponibles es de 60.
OBJETIVO : Maximizar los ingresos totales
VARIABLE DE DECISION:
X1 = Cantidad de auditorías
X2 = Cantidad de liquidaciones
RESTRICCIONES : Tiempo disponible para trabajo directo
Tiempo disponible para trabajo de revisión
Número máximo de liquidaciones
Maximizar ![]()
Sujeto a:
![]()
![]()
![]()
PROBLEMA 3.
Una empresa manufacturera está considerando dedicar su capacidad a fabricar 3 productos; llamémoslos productos 1, 2 y 3. La capacidad disponible de las máquinas que podría limitar la producción se resume en la siguiente tabla:
|
Tipo de Máquina |
Tiempo Disponible (horas máquin) |
|
Fresadora |
500 |
|
Torno |
350 |
|
Rectificadora |
150 |
El número de horas requeridas por cada unidad de los productos respectivos es:
|
Tipo de Máquina |
Producto 1 |
Producto 2 |
Producto 3 |
|
Fresadora |
9 |
3 |
5 |
|
Torno |
5 |
4 |
0 |
|
Rectificadora |
3 |
0 |
2 |
El departamento de ventas indica que el potencial de ventas para los productos 1 y 2 es mayor que la tasa de producción máxima y que el potencial de ventas para el producto 3 es de 20 unidades por semana. La utilidad unitaria sería de 30, 12 y 15 dls., respectivamente, para los productos 1, 2 y 3.
Formúlese el modelo de programación lineal para determinar cuanto debe producir la empresa de cada producto para maximizar la utilidad.
OBJETIVO : Maximizar la utilidad
VARIABLE DE DECISION: Cantidad a fabricar del producto 1. (X1).
Cantidad a fabricar del producto 2. (X2).
Cantidad a fabricar del producto 3. (X3).
RESTRICCIONES : Capacidad disponible para producción de cada máquina (3 restricciones)
Potencial de ventas para el producto 3. (1 restricción)
Maximizar ![]()
Sujeto a:
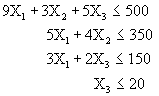
![]()
PROBLEMA 4.
Un expendio de carnes acostumbra preparar carne para hamburguesa con una combinación de carne molida de res y carne molida de cerdo. La carne de res contiene 80 % de carne y 20 % de grasa y le cuesta a la tienda 80 centavos por libra. La carne de cerdo contiene 68 % de carne y 32 % de grasa y cuesta 60 centavos por libra. ¿Qué cantidad de cada tipo de carne debe emplear la tienda por cada libra de carne para hamburguesa si desea minimizar el costo y mantener el contenido de grasa no mayor de 25 %?
OBJETIVO : Minimizar el costo
VARIABLE DE DECISION: Cantidad de carne de res. (X1).
Cantidad de carne de cerdo (X2).
RESTRICCIONES : Contenido de grasa no mayor de 25 %
Contenido de carne molida a producir
Minimizar ![]()
Sujeto a:
![]()
![]()
![]()
PROBLEMA 5.
Formule una dieta para pollos. Suponga que el lote diaria requerido de la mezcla son 100 lbs. La dieta debe contener:
1.- Al menos 0.8 % pero no más de 1.2 % de calcio
2.- Al menos 22 % de proteínas
3.- a lo más 5 % de fibras crudas
Suponga, además, que los principales ingredientes utilizados incluyen maíz, soya y caliza. El contenido nutritivo de estos ingredientes se resume a continuación.
LIBRAS POR LIBRA DE INGREDIENTE
|
IngredienteFibra |
Costo($) por libra |
|||
|
Caliza |
.380 |
.00 |
.00 |
.0164 |
|
Maíz |
.001 |
.09 |
.02 |
.0463 |
|
Soya |
.002 |
.50 |
.08 |
.1250 |
Minimice el costo total para la dieta, determinando la cantidad de cada ingrediente que debe utilizarse.
OBJETIVO : Minimizar el costo total de la dieta (100 lbs.)
VARIABLE DE DECISION: Contenido de caliza. (X1).
Contenido de maíz (X2).
Contenido de soya (X3).
RESTRICCIONES : Contenidos nutritivos (4 restricciones).
Contenido de la mezcla de 100 lbs. (1 restricción)![]()
Minimizar ![]()
Sujeto a:
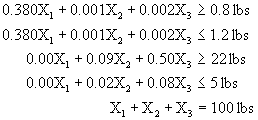
![]()
PROBLEMA 6.
Una compañía distribuidora de agua tiene 3 depósitos con entrada diaria estimada de 15, 20 y 25 millones de litros de agua respectivamente. Diariamente tiene que abastecer 4 áreas A, B, C y D, las cuales tienen una demanda esperada de 8, 10, 12 y 15 millones de litros de agua, respectivamente. El costo de bombeo por millón de litros de agua es como sigue:
|
DEPÓSITO |
ÁREA |
|||
|
A |
B |
C |
D |
|
|
1 |
2 |
3 |
4 |
5 |
|
2 |
3 |
2 |
5 |
2 |
|
3 |
4 |
1 |
2 |
3 |
Minimice el costo total de suministro de agua de los depósitos a las áreas.
OBJETIVO : Minimizar el costo total de suministro de agua de los depósitos a las áreas.
VARIABLES DE DECISION: Cantidad de agua que se envía de cada depósito a cada área.
RESTRICCIONES : Entradas de agua disponible. (3 restricciones)
Necesidades de agua de las áreas. (4 restricciones)
Minimizar
![]()
Sujeto a: 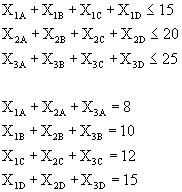
![]()
![]()
PROBLEMA 7.
Una compañía de minas opera 3 minas. El mineral de cada una de ellas se separa antes embarcarse en 2 grados (tipos). La cantidad diaria de producción de las minas así como sus costos diarios de operación son los siguientes:
|
|
Mineral Grado Alto (ton/día) |
Mineral Grado Bajo (ton/día) |
Costo ($!,000/día) |
|
Mina I |
4 |
4 |
20 |
|
Mina II |
6 |
4 |
22 |
|
Mina III |
1 |
6 |
18 |
La compañía se comprometió a entregar 54 toneladas de mineral de grado alto y 65 toneladas de mineral de grado bajo para fines de la semana siguiente (7 días disponibles de operación). Además, desea determinar el número de días que la mina debería operar durante la siguiente semana si debe cumplir su compromiso a un costo mínimo.
OBJETIVO : Minimizar el costo de extracción mineral.
VARIABLE DE DECISION: Días de operación en cada mina.
X1=Número de días de operación de la mina I
X2=Número de días de operación de la mina II
X3=Número de días de operación de la mina III
RESTRICCIONES : Tiempo disponible (7 días) (3 restricciones)
Cantidad de mineral alto grado (1 restricción)
Cantidad de mineral bajo grado (1 restricción)
Minimizar ![]()
Sujeto a:
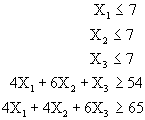
![]()
EJEMPLO 8.
Jack Bienstaulk tiene a su cargo la compra de mercancías enlatadas para el servicio de alimentos GAGA en una gran universidad. Él sabe cuál será la demanda durante el transcurso del año escolar y ha estimado también los precios de compra. En la figura se muestran estos datos. Puede comprar anticipadamente y almacenar para evitar los aumentos de precios, pero existe un costo de mantener inventario de $0.20 por caja, por mes, aplicado al inventario en existencia al final del mes. Elabore un PL que minimice el costo y que ayude a Jack a determinar el momento de sus compras, Sugerencia: Supóngase que Pt es el número de cajas compradas en el mes t y que It es el número de cajas en existencias al final del mes t.
Datos de la demanda y el costo
|
SEP. |
OCT. |
NOV. |
DIC. |
ENE. |
FEB. |
MAR. |
ABR. |
MAY. |
|
|
Demandas (cajas ) |
1000 |
900 |
850 |
500 |
600 |
1000 |
1000 |
1000 |
500 |
|
costo por caja |
$20 |
$20 |
$20 |
$21 |
$21 |
$21 |
$23 |
$23 |
$23 |
OBJETIVO: Minimizar el costo total (costo de compra e inventarios)
VARIABLES: Pt =Cantidad de cajas compradas en el mes t. (t=1,2,… 9)
It = Cantidad de cajas en existemcia en el mes t (t=1,2,…8)
RESTRICCIONES: Ecuaciones de demanda e inventarios por mes (9 restricciones)

EJEMPLO 9.
Para una cafetería que trabaja 24 horas se requieren las siguientes meseras:
|
HORAS DEL DÍA |
NÚMERO MÍNIMO DE MESERAS |
|
2-6 |
4 |
|
6-10 |
8 |
|
10-14 |
10 |
|
14-18 |
7 |
|
18-22 |
12 |
|
22-2 |
4 |
Cada mesera trabaja 8 horas consecutivas por día con horarios de entrada 2, 6, 10, 14, 18 y 22 horas. El objetivo es encontrar el número más pequeño requerido para cumplir los requisitos anteriores. Formule el problema como un modelo de programación lineal.
OBJETIVO: Minimizar el número total de meseras requeridas.
VARIABLES DE DECISIÓN: X1= Número de meseras que entran a las 2
X2= Número de meseras que entran a las 6
X3= Número de meseras que entran a las 10
X4= Número de meseras que entran a las 14
X5= Número de meseras que entran a las 18
X6= Número de meseras que entran a las 22
RESTRICCIONES: Cantidad de meseras requeridas en el horario de 2-6 (4 meseras)
Cantidad de meseras requeridas en el horario de 6-10 (8 meseras)
Cantidad de meseras requeridas en el horario de 10-14 (10 meseras)
Cantidad de meseras requeridas en el horario de 14-18 (7 meseras)
Cantidad de meseras requeridas en el horario de 18-22 (12 meseras)
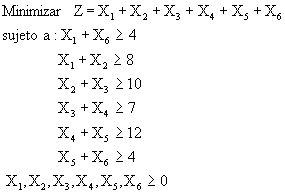 Cantidad de meseras requeridas en el horario de 22-2 (4 meseras)
Cantidad de meseras requeridas en el horario de 22-2 (4 meseras)
10. Una cadena de restaurantes de servicio rápido desea construir cuatro tiendas. Anteriormente, la cadena ha empleado sies diferentes compañías y, estando satisfecha con todas ellas, las ha invitado a concursar para cada trabajo. Las ofertas finales en miles de dólares son las que se muestran.
|
tienda |
constructoras |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
85.3 |
88 |
87.5 |
82.4 |
89.1 |
86.1 |
|
2 |
78.9 |
77.4 |
77.4 |
76.5 |
79.3 |
78.3 |
|
3 |
82 |
81.3 |
82.4 |
80.6 |
83.5 |
81.7 |
|
4 |
84.3 |
84.6 |
86.2 |
83.3 |
84.4 |
85.5 |
Ya que la cadena desea tener listos los nuevos establecimientos tan pronto como sea posible otorgará cuando más un trabajo a cada compañía constructora, ¿que asignación da como resultado un costo total mínimo para la cadena de restaurantes?
OBJETIVO: Minimizar el costo de construcción de las tiendas
VARIABLES: X11 = Asignar la tienda 1 a la constructora 1
X12 = Asignar la tienda 1 a la constructora 2
X13 = Asignar la tienda 1 a la constructora 3
...................................................................
X46 = Asignar la tienda 4 a la constructora 6
RESTRICCIONES: Asignar la tienda 1
Asignar la tienda 2
Asignar la tienda 3
Asignar la tienda 4
Máximo una tienda para constructora 1
Máximo una tienda para constructora 2
Máximo una tienda para constructora 3
Máximo una tienda para constructora 4
Máximo una tienda para constructora 5
Máximo una tienda para constructora 6
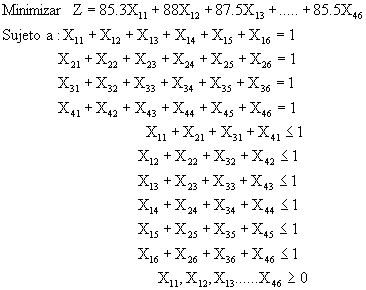
SOLUCION DE PROBLEMAS DE PROGRAMACION LINEAL POR EL METODO GRAFICO.
El método gráfico se emplea para resolver problemas que presentan sólo 2 variables de decisión. El procedimiento consiste en trazar las ecuaciones de las restricciones en un eje de coordenadas X1, X2 para tratar de identificar el área de soluciones factibles (soluciones que cumplen con todas las restricciones).
La solución óptima del problema se encuentra en uno de los vértices de esta área de soluciones creada, por lo que se buscará en estos datos el valor mínimo o máximo del problema.
EJEMPLO 1:
Una compañía de auditores se especializa en preparar liquidaciones y auditorías de empresas pequeñas. Tienen interés en saber cuantas auditorías y liquidaciones pueden realizar mensualmente para maximizar sus ingresos. Se dispone de 800 horas de trabajo directo y 320 horas para revisión. Una auditoría en promedio requiere de 40 horas de trabajo directo y 10 horas de revisión, además aporta un ingreso de 300 dls. Una liquidación de impuesto requiere de 8 horas de trabajo directo y de 5 horas de revisión, produce un ingreso de 100 dls. El máximo de liquidaciones mensuales disponibles es de 60.
OBJETIVO : Maximizar el ingreso total.
VARIABLE DE DECISION: Cantidad de auditorías (X1).
Cantidad de liquidaciones (X2).
RESTRICCIONES : Tiempo disponible de trabajo directo
Tiempo disponible de revisión
Número máximo de liquidaciones.
Maximizar ![]()
Sujeto a:
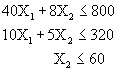
![]()

La solución óptima siempre se encuentra en uno de los vértices del conjunto de soluciones factibles. Se analizan estos valores en la función objetivo. El vértice que representa el mejor valor de la función objetivo será la solución óptima.
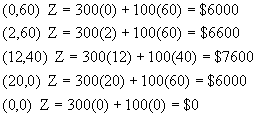

EJEMPLO 2.
Un departamento de publicidad tiene que planear para el próximo mes una estrategia de publicidad para el lanzamiento de una línea de T.V. a color tiene a consideración 2 medios de difusión: La televisión y el periódico.
Los estudios de mercado han mostrado que:
1. La publicidad por T.V. Llega al 2 % de las familias de ingresos altos y al 3 % de las familias de ingresos medios por comercial.
2. La publicidad en el periódico llega al 3 % de las familias de ingresos altos y al 6 % de las familias de ingresos medios por anuncio.
La publicidad en periódico tiene un costo de 500 dls. por anuncio y la publicidad por T.V. tiene un costo de 2000 dls. por comercial. La meta es obtener al menos una presentación como mínimo al 36 % de las familias de ingresos altos y al 60 % de las familias de ingresos medios minimizando los costos de publicidad.
OBJETIVO : Minimizar los costos de publicidad.
VARIABLE DE DECISION: Anuncios para las familias de ingreso alto (X1).
Anuncios para las familias de ingreso medio (X2).
RESTRICCIONES : Porcentaje de presentación.
Minimizar ![]()
Sujeto a:
![]()
![]()

SOLUCION OPTIMA:

EJEMPLO 3.
Un expendio de carnes acostumbra preparar carne para hamburguesa con una combinación de carne molida de res y carne molida de cerdo. La carne de res contiene 80 % de carne y 20 % de grasa y le cuesta a la tienda 80 centavos por libra. La carne de cerdo contiene 68 % de carne y 32 % de grasa y cuesta 60 centavos por libra. ¿Qué cantidad de cada tipo de carne debe emplear la tienda por cada libra de carne para hamburguesa si desea minimizar el costo y mantener el contenido de grasa no mayor de 25 %?
Minimizar ![]()
Sujeto a:
![]()
![]()
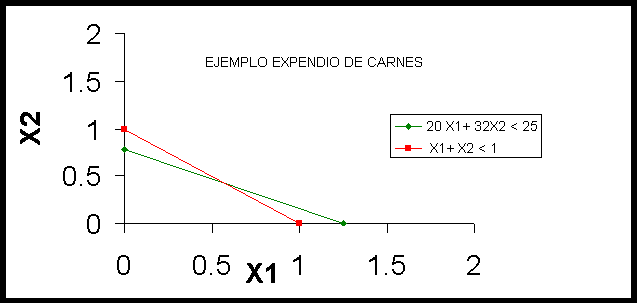
SOLUCION OPTIMA:
![]()

TAREA UNIDAD I
ELABORE LOS MODELOS DE LOS SIGUIENTES PROBLEMAS
1. Wood Walker es un fabricante de muebles independiente. Hace tres estilos diferentes de mesas, A, B, C. Cada modelo de mesa requiere de una cierta cantidad de tiempo para el corte de las piezas, su montaje y pintura. Wood puede vender todas las unidades que fabrica. Es más, el modelo B se puede vender sin pintar. Utilizando los datos de la figura, formule un modelo de PL que ayude a Wood a determinar la mezcla de productos que maximizará sus utilidades.
|
MODELO |
TIEMPO POR MESA (HORAS) |
UTILIDAD POR MESA |
||
|
DE CORTE |
DE ENSAMBLADO |
DE PINTURA |
||
|
A |
1 |
2 |
4 |
$35 |
|
B |
2 |
4 |
4 |
40 |
|
B sin pintar |
2 |
4 |
0 |
20 |
|
C |
3 |
7 |
5 |
50 |
|
CAPACIDAD (horas/mes) |
200 |
300 |
150 |
|
2. McNaughton, Inc. produce dos salsas para bistec: Diablo picante y Barón Rojo suave. Ambas salsas se hacen mezclando dos ingredientes A y B. Se permite un cierto nivel de flexibilidad en las fórmulas de estos productos. En la figura se presentan los porcentajes permisibles, junto con datos de ingresos y costos. Se pueden comprar hasta 40 cuartos de A y 30 de B. McNaughton puede vender todas las salsas que produzca. Elabore un PL cuyo objetivo sea maximizar el ingreso neto proveniente de la venta de las salsas.
Porcentajes permisibles para McNaughton, Inc.
|
SALSA |
INGREDIENTE |
PRECIO DE VENTA POR CUARTO |
|
|
A |
B |
||
|
Diablo picante |
por lo menos un 25% |
por lo menos un 50% |
$3.35 |
|
Barón Rojo |
cuando mucho un 75% |
* |
2.85 |
|
Costo por cuarto |
$1.60 |
$2.59 |
|
3. Un cierto restaurante opera 7 días ala semana. A las camareras se les contrata para trabajar 6 horas diarias. El contrato del sindicato especifica que cada camarera tiene que trabajar 5 días consecutivos y después de tener 2 días consecutivos de descanso. Cada camarera recibe el mismo sueldo semanal. En la figura se presentan las necesidades de contratación. Supóngase que este ciclo de necesidades se repite en la forma indefinida y no toma en cuenta el hecho de que el número de camareras contratadas tiene que ser un número entero. El gerente desea encontrar un programa de empleo que satisfaga estas necesidades a un costo mínimo. Formule este problema como un programa lineal.
Necesidades de contratación de camareras
|
DIA |
NUMERO MINIMO DE HORAS DE CAMARERAS NECESARIAS |
|
LUNES |
150 |
|
MARTES |
200 |
|
MIERCOLES |
400 |
|
JUEVES |
300 |
|
VIERNES |
700 |
|
SABADO |
800 |
|
DOMINGO |
300 |
4. La E.L. Griffith Company es un fabricante grande de zapatos, ubicado en la región del medio oeste en los Estados Unidos de Norteamérica. La Griffith se especializa en la fabricación de botas vaqueras y no vende en forma directa al público sino que en cambio, vende a través de expendios, al menudeo. Según las fluctuaciones en los costos de diversos componentes, la compañía ha observado que el costo de producción varía de un mes a otro. Debido a estas variaciones en los costos (y bajo el costo de manejo y almacenamiento que es de $1.00 por mes por par de botas), la Griffith considera que resulta conveniente fabricar pares de botas en exceso en algunos meses para venderlas en meses posteriores. Los administradores de la Griffith han pronosticado la demanda y los costos para los siguientes siete meses como se muestra en la tabla. La compañía desea programar la producción para minimizar los costos totales de producción y manejo. Plantee un modelo de PL para el problema. (No existe restricción de capacidad sobre la producción o sobre el almacenamiento)
|
Mes |
Demanda pronosticada |
Costo proyectado (por par) |
|
1 |
150,000 |
36.00 |
|
2 |
110,000 |
42.00 |
|
3 |
180,000 |
38.00 |
|
4 |
100,000 |
40.00 |
|
5 |
200,000 |
35.00 |
|
6 |
180,000 |
39.00 |
|
7 |
110,000 |
37.00 |
5. El gerente de la línea de producción de una empresa electrónica debe asignar personal a cinco tareas. Existen cinco operadores disponibles para asignarlos. El gerente de la línea tiene a su disposición datos de prueba que reflejan una calificación numérica de productividad para cada uno de los cinco trabajadores en cada uno de los trabajos. Estos datos se obtuvieron a través de un examen de operación y prueba administrado por el departamento de ingeniería industrial (véase la tabla).
|
Número de operador |
Número de trabajo |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
12 |
16 |
24 |
8 |
2 |
|
2 |
6 |
8 |
20 |
14 |
6 |
|
3 |
10 |
6 |
16 |
18 |
12 |
|
4 |
2 |
4 |
2 |
24 |
20 |
|
5 |
7 |
10 |
6 |
6 |
18 |
Suponiendo que un operador pueda ejecutar un solo trabajo, plantee un modelo que conduzca a la asignación óptima de tareas.
6. Una compañía de las instalaciones A, B y C suministra a los distribuidores D, E, F, y G. Las capacidades mensuales son 20, 30 y 45 unidades, respectivamente. Los requerimientos mensuales de los distribuidores son 10, 15, 40 y 30 unidades, respectivamente. Los costos unitarios de envío son los siguientes:
|
Desde |
Hacia |
|||
|
D |
E |
F |
G |
|
|
A |
$5 |
$10 |
$5 |
$ 0 |
|
B |
$5 |
$9 |
$5 |
$10 |
|
C |
$10 |
$10 |
$15 |
$ 5 |
Determinar un plan óptimo de distribución. ¿Cuál es el mínimo costo de transporte?
7. Una compañía manufactura tres productos diferentes A, B y C que son vendidos a $5, $10 y $20 por unidad, respectivamente. Se requieren cuatro diferentes tipos de materia prima para su producción, de acuerdo a la siguiente tabla. Formule un programa lineal que maximice la utilidad de la empresa. (Recuerde: Utilidad = Ingresos - Costos)
|
MATERIA PRIMA |
COSTO/UNIDAD |
UNIDADES DE MATERIA PRIMA POR UNIDAD DE PRODUCTO |
SUMINISTRO DISPONIBLE |
||
|
A |
B |
C |
|||
|
1 |
$2 |
0 |
1 |
2 |
100 |
|
2 |
$1 |
1 |
2 |
1 |
200 |
|
3 |
$0.50 |
4 |
6 |
10 |
400 |
|
4 |
$2 |
0 |
0 |
2 |
100 |
8. Un entrenador sabe que su equipo avanza un promedio de 3 yardas en una jugada por tierra que consume un promedio de 40 segundos. En una jugada de pase, la ganancia promedio es de 5 yardas en 15 segundos. Quedan 1 minuto y 55 segundos de juego en un partido y 28 yardas para anotar y están perdiendo por 5 puntos, sabe además, que pierde el balón un promedio de una vez cada 10 corridas y una vez en cada 3 pases. ¿Qué combinación de carreras y pases debe usar para lograr la anotación con la menor probabilidad de perder el balón?
9. Se utiliza un horno eléctrico para fundir hierro y producir fundiciones de hierro gris y se requiere una carga de dos toneladas (4,000 libras). Diversos materiales dan un producto final que satisface las especificaciones. El problema consiste en seleccionar la alimentación que satisfaga las especificaciones con un costo mínimo. El proceso debe satisfacer las siguientes especificaciones de materiales:
|
MÍNIMO |
MÁXIMO |
|
|
CARBONO (%) |
3.25 |
3.40 |
|
SÍLICE (%) |
2.05 |
2.25 |
Los materiales disponibles para la alimentación son:
|
MATERIAL |
% CARBONO |
%SÍLICE |
COSTO |
|
CHATARRA A |
0.45 |
0.10 |
$60/TONELADA |
|
CHATARRA B |
0.40 |
0.15 |
$63/TONELADA |
|
CHATARRA C |
3.50 |
2.30 |
$68/TONELADA |
|
SOBRANTES |
3.30 |
2.20 |
$40/TONELADA |
|
BRIQUETAS (C) |
100 |
0 |
$0.30/LIBRA |
|
BRIQUETAS (Si) |
0 |
100 |
$0.50/LIBRA |
10. Una comunidad ha reunido $250 000 para desarrollar nuevas áreas de eliminación de desechos. Hay siete sitios disponibles, cuyos costos de desarrollo y capacidades se muestran a continuación. ¿Qué sitios deberá desarrollar la comunidad?
|
Sitio |
A |
B |
C |
D |
E |
F |
G |
|
Capacidad, ton/semana |
20 |
17 |
15 |
15 |
10 |
8 |
5 |
|
Costo, $1000 |
145 |
92 |
70 |
70 |
84 |
14 |
47 |
RESUELVA POR EL MÉTODO GRÁFICO
1. La compañía Swelte Glove manufactura y vende dos productos. La compañía obtiene una utilidad de $12 por utilidad del producto 1 y $4 por unidad del producto 2 que se vendan. Las horas de trabajo que se requieren para los productos en cada uno de los tres departamentos de producción se sintetizan en la figura. Los supervisores de estos departamentos han estimado que durante el próximo mes estarán disponibles las siguientes horas de trabajo: 800 en el departamento 1, 600 en el departamento 2 y 2000 en el departamento 3. Suponiendo quiera maximizar las utilidades, formule el modelo de programación lineal de este problema.
Datos de producción de la compañía Swelte Glove
|
DEPARTAMENTO |
PRODUCTO 1 |
PRODUCTO 2 |
|
1 |
1 |
2 |
|
2 |
1 |
3 |
|
3 |
2 |
3 |
2. La LIlac Vitamin Co. planea producir una cápsula de vitamina barata usando dos ingredientes básicos, X y Y. Cada unidad de X contiene 0,5 miligramos (mg) de vitamina A, 1,0 mg de vitamina B1, 0,2 mg de vitamina B2 y 0,5 mg de vitamina D. Cada unidad de Y contiene 0,5 mg de vitamina A, 0,3 mg de vitamina B1, 0,6 mg vitamina B2 y 0,20 mg de vitamina D. El costo unitario de X es $0,30 y el de Y es $0,50. Cada cápsula tiene que contener como mínimo 2 mg de vitamina A, 3 mg de vitamina B1, 1,2 mg de vitamina B2 y 2 mg de vitamina D.
(a) Construir un modelo de programación lineal para la Lilac Vitamin Company.
(b) Encontrar la combinación óptima de X y Y que minimice el costo usando el método gráfico.
3. Resuelva el problema no. 8 de la tarea de formulación de problemas.